Difference between revisions of "Curbe Bezier"
From linux360
m (→Curba Bézier liniară) |
|||
| Line 40: | Line 40: | ||
<math>P(t) = B_{0,1}P_{0} + B_{1,1}P_{1} \iff P(t) = (1-t)P_{0} + tP_{1}, t \in [0,1]</math> | <math>P(t) = B_{0,1}P_{0} + B_{1,1}P_{1} \iff P(t) = (1-t)P_{0} + tP_{1}, t \in [0,1]</math> | ||
| − | Reprezentarea grafică este doar o linie şi din acest motiv nu este aproape deloc folosită. | + | Reprezentarea grafică este doar o linie şi din acest motiv această formă nu este aproape deloc folosită. |
| + | |||
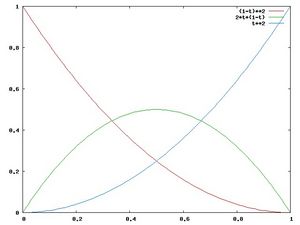
| + | [[Image:Bezier_3.jpg |thumb|300px| Fig. 4 - Graficul polinoamelor Bernstein de ordinul 3]] | ||
| − | |||
===Curba Bézier pătratică=== | ===Curba Bézier pătratică=== | ||
Curba Bézier pătratică sau de ordinul 2 este o curbă dată prin trei puncte, punctul din mijloc fiind un punct de control care nu se află pe curbă, dar care influenţează aspectul acesteia. | Curba Bézier pătratică sau de ordinul 2 este o curbă dată prin trei puncte, punctul din mijloc fiind un punct de control care nu se află pe curbă, dar care influenţează aspectul acesteia. | ||
Revision as of 18:02, 5 November 2006
O curbă Bézier este o curbă parametrică inventată de inginerul francez Pierre Bézier şi făcută publică în anul 1962. Bézier a folosito în procesul de design al automobilelor. Curbele Bézier sunt foarte importante şi pentru domeniul tehnologiei informaţiei, fiind folosite în construcţia fonturilor TrueType.
Contents
Polinoame Bernstein
Polinoamele Bernstein stau la baza curbelor Bézier. Acestea poartă numele matematicianului ucrainian Sergei Natanovich Bernstein.
Pentru a determina polinoamele Bernstein de orice grad se porneşte de la polinomul Bernstein de ordinul zero.
<math>1 = 1</math>
Apoi se scade din ambele părţi o varibilă t şi obţinem:
<math>1-t = 1-t \iff (1-t) + t = 1</math>
Ultima expresie este o combinaţie liniară a polinoamelor Bernstein de bază de ordinul unu. Polinoamele sunt:
<math>\begin{cases} B_{0,1} = 1-t \\ B_{1,1} = t\end{cases}</math>
Acum putem obţine polinoame Bernstein de orice grad prin ridicarea la putere a ultimei expresii:
<math>((1-t) + t)^{2} = 1 \iff (1-t)^{2} + 2t(1-t) + t^2 = 1</math>
Obţinem astfel polinoamele Berstein de bază de ordinul doi: <math>\begin{cases}B_{0,2} = (1-t)^2 \\ B_{1,2} = 2t(1-t) \\ B_{2,2} = t^2 \end{cases}</math>
Foarte interesante şi utile sunt graficele polinoamelor Bernstein, pentru înţelegerea modului în care "funcţionează" curbele Bézier.
Definirea unei curbe Bézier
O curbă Bézier de ordinul n se defineşte, cu ajutorul a n puncte, după cum urmează: <math>P(t) = \sum_{k=0}^N B_{k,N}*P_{k}</math>, unde <math>B_{k,N}</math> este polinomul de indice k, Bernstein şi de ordin N. <math>P_{k}</math> sunt puncte în plan, adică vectori cu două componente <math>(x_{k}, y_{k})</math>.
Curba Bézier liniară
Curba Bézier liniară este definită folosind polinoamele Bernstein de ordinul 1: <math>\begin{cases} B_{0,1} = 1-t \\ B_{1,1} = t\end{cases}</math>
Ecuaţia:
<math>P(t) = B_{0,1}P_{0} + B_{1,1}P_{1} \iff P(t) = (1-t)P_{0} + tP_{1}, t \in [0,1]</math>
Reprezentarea grafică este doar o linie şi din acest motiv această formă nu este aproape deloc folosită.
Curba Bézier pătratică
Curba Bézier pătratică sau de ordinul 2 este o curbă dată prin trei puncte, punctul din mijloc fiind un punct de control care nu se află pe curbă, dar care influenţează aspectul acesteia.