Curbe Bezier

Fig. 1 - Graficul polinoamelor Bernstein de ordinul 0

Fig. 2 - Graficul polinoamelor Bernstein de ordinul 1

Polinoame Bernstein

Polinoamele Bernstein stau la baza curbelor Bézier. Acestea poartă numele matematicianului ucrainian Sergei Natanovich Bernstein.

Pentru a determina polinoamele Bernstein de orice grad se porneşte de la polinomul Bernstein de ordinul zero.

<math>1 = 1</math>

Apoi se scade din ambele părţi o varibilă t şi obţinem:

<math>1-t = 1-t \iff (1-t) + t = 1</math>

Ultima expresie este o combinaţie liniară a polinoamelor Bernstein de bază de ordinul unu. Polinoamele sunt:

<math>\begin{cases} B_{0,1} = 1-t \\ B_{1,1} = t\end{cases}</math>

Acum putem obţine polinoame Bernstein de orice grad prin ridicarea la putere a ultimei expresii:

<math>((1-t) + t)^{2} = 1 \iff (1-t)^{2} + 2t(1-t) + t^2 = 1</math>

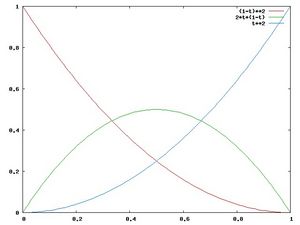
Obţinem astfel polinoamele Berstein de bază de ordinul doi: <math>\begin{cases}B_{0,2} = (1-t)^2 \\ B_{1,2} = 2t(1-t) \\ B_{2,2} = t^2 \end{cases}</math>

Fig. 3 - Graficul polinoamelor Bernstein de ordinul 2

Fig. 4 - Graficul polinoamelor Bernstein de ordinul 3

Foarte interesante şi utile sunt graficele polinoamelor Bernstein, pentru înţelegerea modului în care "funcţionează" curbele Bézier.