Difference between revisions of "Curbe Bezier"
From linux360
(Interpolarea a trei puncte) |
m (→Interpolarea a trei puncte: Enabled syntax highlighting) |
||
| Line 117: | Line 117: | ||
În continuare codul sursă Java care implementează interpolarea a trei puncte folosind o curbă Bézier de ordinul doi. | În continuare codul sursă Java care implementează interpolarea a trei puncte folosind o curbă Bézier de ordinul doi. | ||
| − | + | <code><java/>import java.awt.geom.Point2D; | |
| − | < | ||
/** | /** | ||
| Line 187: | Line 186: | ||
System.out.println(bezPoints[2]); | System.out.println(bezPoints[2]); | ||
} | } | ||
| − | }</ | + | }</code> |
| + | |||
===Interpolarea a patru puncte=== | ===Interpolarea a patru puncte=== | ||
[[Category:Pending]] | [[Category:Pending]] | ||
Revision as of 15:53, 13 November 2006
O curbă Bézier este o curbă parametrică inventată de inginerul francez Pierre Bézier şi făcută publică în anul 1962. Bézier a folosito în procesul de design al automobilelor. Curbele Bézier sunt foarte importante şi pentru domeniul tehnologiei informaţiei, fiind folosite în construcţia fonturilor TrueType.
Contents
Polinoame Bernstein
Polinoamele Bernstein stau la baza curbelor Bézier. Acestea poartă numele matematicianului ucrainian Sergei Natanovich Bernstein.
Pentru a determina polinoamele Bernstein de orice grad se porneşte de la polinomul Bernstein de ordinul zero.
<math>1 = 1</math>
Apoi se scade din ambele părţi o varibilă t şi obţinem:
<math>1-t = 1-t \iff (1-t) + t = 1</math>
Ultima expresie este o combinaţie liniară a polinoamelor Bernstein de bază de ordinul unu. Polinoamele sunt:
<math>\begin{cases} B_{0,1} = 1-t \\ B_{1,1} = t\end{cases}</math>
Acum putem obţine polinoame Bernstein de orice grad prin ridicarea la putere a ultimei expresii:
<math>((1-t) + t)^{2} = 1 \iff (1-t)^{2} + 2t(1-t) + t^2 = 1</math>
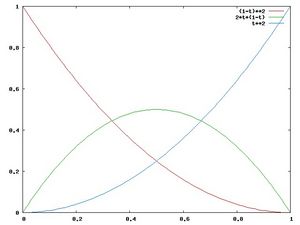
Obţinem astfel polinoamele Berstein de bază de ordinul doi: <math>\begin{cases}B_{0,2} = (1-t)^2 \\ B_{1,2} = 2t(1-t) \\ B_{2,2} = t^2 \end{cases}</math>
Foarte interesante şi utile sunt graficele polinoamelor Bernstein, pentru înţelegerea modului în care "funcţionează" curbele Bézier.
Definirea unei curbe Bézier
O curbă Bézier de ordinul n se defineşte, cu ajutorul a n puncte, după cum urmează: <math>P(t) = \sum_{k=0}^N B_{k,N}*P_{k}</math>, unde <math>B_{k,N}</math> este polinomul Bernstein de indice k şi de ordin N. <math>P_{k}</math> sunt puncte în plan, adică vectori cu două componente <math>(x_{k}, y_{k})</math>.
Curba Bézier liniară
Curba Bézier liniară este definită folosind polinoamele Bernstein de ordinul 1: <math>\begin{cases} B_{0,1} = 1-t \\ B_{1,1} = t\end{cases}</math>
Ecuaţia:
<math>P(t) = B_{0,1}P_{0} + B_{1,1}P_{1} \iff P(t) = (1-t)P_{0} + tP_{1}, t \in [0,1]</math>
Reprezentarea grafică este doar o linie şi din acest motiv această formă nu este aproape deloc folosită.
Curba Bézier pătratică
Curba Bézier pătratică sau de ordinul doi este o curbă dată prin trei puncte, punctul din mijloc fiind un punct de control care nu se află pe curbă, dar care influenţează aspectul acesteia.
Aceasta foloseşte polinoamele Bernstein de ordinul doi:
<math>\begin{cases}B_{0,2} = (1-t)^{2} \\ B_{1,2} = 2t(1-t) \\ B_{2,2} = t^2\end{cases}</math>
Ecuaţia curbei este:
<math>P(t) = B_{0,2}P_0 + B_{1,2}P_1 + B_{2,2}P_2 \iff P(t) = (1-t)^{2}P_0 + 2t(1-t)P_1 + t^{2}P_2</math>
În anumite documente ecuaţiile sunt date în funcţie de puterile lui t, lucru care aduce confuzie, de aceea prezint în continuare şi această formă.
<math>P(t) = P_0 - P_0t^2 +2tP_1-2t^{2}P_1 + t^{2}P_2 \iff P(t) = t^{2}(P_2 - P_0 - 2P_1) +t2P_1 + P_0</math>
Se fac notaţiile: <math>\begin{cases}A = P_2 - 2P_1 - P_0 \\ B = 2P_1 \\ C = P_0\end{cases} \iff \begin{cases}A = P_2 - B - C \\ B = 2P_1 \\ C = P_0 \end{cases}</math>
Şi ecuaţia capătă următoarea formă: <math>P(t) = At^2 + Bt + C</math>
Ca şi proprietăţi ale curbei trebuie să subliniez următoarele:
<math>P(0) = P_0</math>
<math>P(1) = P_2</math>
Acest lucru poate fi uşor observat şi motivat cu ajutorul graficelor din figura 3.
Curba Bézier cubică
Curba Bézier cubică sau de ordinul trei este dată prin patru puncte <math>P_0, P_1, P_2</math> şi <math>P_4</math>. <math>P_1</math> şi <math>P_2</math> sunt puncte de control ale curbei.
Pentru a putea scrie ecuaţia curbei scriem mai întâi ecuaţiile polinoamelor Bernstein de ordinul trei:
<math>\begin{cases}B_{0,3} = (1-t)^{3} \\ B_{1,3} = 3t(1-t)^2 \\ B_{2,3} = 3t^2(1-t) \\ B_{3,3} = t^{3} \end{cases}</math>.
Ecuaţia curbei:
<math>P(t) = B_{0,3}P_0 + B_{1,3}P_1 + B_{2,3}P_2 + B_{3,3}P_3 \iff P(t) = (1-t)^{3}P_0 + 3t(1-t)^2P_1 + 3t^2(1-t)P_2 + t^{3}P_3</math>
Scriem în funcţie de puterile lui t şi obţinem:
<math>P(t) = t^3(P_3 - 3P_2 + 3P_1 - P_0) + t^2(3P_2 - 6P_1 + 3P_0) + t(3P_1 - 3P_0) + P_0</math>
Se fac notaţiile:
<math>\begin{cases}A = P_3 - 3P_2 + 3P_1 - P_0 \\ B = 3P_2 - 6P_1 + 3P_0 \\ C = 3P_1 - 3P_0 \end{cases} \iff \begin{cases}A = P_3 - P_0 - B - C \\ B = 3(P_2 - P_1) - C \\ C = 3(P_1 - P_0)\end{cases}</math>
Ecuaţia curbei în funcţie de A, B şi C: <math>P(t) = At^3 + Bt^2 + Ct+P_0</math>
Desenarea unei curbe Bézier
Probleme de interpolare folosind curbe Bézier
Interpolare: Interpolarea reprezintă o metodă matematică de a creea date care lipsesc.
Multe persoane nu se simt confortabil să deseneze curbe Bézier folosind acele controale care nu se află pe curbă. Este un pic nenatural, deşi în aplicaţii complexe ale curbelor acele controale devin mult mai importante şi uşurează foarte mult munca. De exemplu atunci când se doreşte alipirea a două curbe Bézier, dorind păstrarea continuităţii punctul de control al celei de-a doua curbe se modifică astfel încât să fie coliniar cu punctul de control al primei curbe şi punctul comun celor două curbe.
În cazurile în care cunoaştem înainte puncte de pe curbă şi vrem să găsim ecuaţia curbei care trece prin acele puncte, trebuie să găsim o metodă de interpolare.
Interpolarea a trei puncte
Cunoaştem trei puncte <math>P_1</math>, <math>P_C</math> şi <math>P_3</math>. Dorim să găsim o curbă Bézier care să trecă prin aceste trei puncte. Este clar că <math>P_1</math> şi <math>P_3</math> sunt două dintre punctele care definesc curba Bézier şi mai trebuie să aflăm un punct asfel încât să definim o curbă Bézier de ordinul doi, dar care să treacă prin <math>P_C</math>.
Pentru că <math>P_C</math> se află pe curbă, înseamnă că satisface ecuaţia ei.
<math>P_C = P_1B_{0,2}(t_c) + P_2B_{1,2}(t_c) + P_3B_{2,2}(t_c)</math>, unde <math>P_2</math> este punctul pe care trebuie să-l aflăm. Ţinând cont că P_C este definit pentru un anumit <math>t_c</math>, trebuie să-l aflăm pentru a putea afla <math>P_2</math> folosind doar ecuaţia liniară scrisă anterior.
O metodă bună de a aproxima t-ul cunoscând un punct de pe curbă este printr-un raport al distanţelor.
<math>t_c = \frac{dist(P_1,P_C)}{dist(P_1,P_C)+dist(P_C,P_3)}</math>
Cunoscând <math>t_c</math> putem scrie soluţia ecuaţiei:
<math>P_2 = \frac{P_C - P_1B_{0,2}(t_c) - P_3B_{2,2}(t_c)}{B_{1,2}(t_c)}</math>
În continuare codul sursă Java care implementează interpolarea a trei puncte folosind o curbă Bézier de ordinul doi.
<java/>import java.awt.geom.Point2D;
/**
* * @author cristi */
public class BezierUtils {
/** * Functia ia ca parametri trei puncte de pe curba si intoarce un array de * trei elemente care sunt punctele pentru definirea curbei Bezier de ordinul * doi care trece prin cele trei puncte (Interpolare). * @param x0 Primul punct de pe curba * @param x3 Al doilea punct de pe curba * @param x2 Al treilea punct de pe curba * @return Point2D.Float[] */ public static Point2D.Float[] getQuadInterpPoints(Point2D.Float x0, Point2D.Float x3, Point2D.Float x2) { Point2D.Float[] result = new Point2D.Float[3]; result[0] = new Point2D.Float(x0.x, x0.y); result[2] = new Point2D.Float(x2.x, x2.y); result[1] = new Point2D.Float(); double t = x0.distance(x3) / (x0.distance(x3) + x3.distance(x2)); result[1].x = ((float)((x3.getX() - fq2(t)*x2.getX() - fq0(t)*x0.getX())/fq1(t))); result[1].y = ((float)((x3.getY() - fq2(t)*x2.getY() - fq0(t)*x0.getY())/fq1(t))); return result; }
/** * Polinomul Bernstein de indice 0 si ordin 2 * @param t * @return * returneaza valoarea polinomului Bernstein B_{k,n}(t) in t, k - indice, n - ordin */ private static double fq0(double t) { return Math.pow((1-t), 2); }
/** * Polinomul Bernstein de indice 1 si ordin 2 * @param t * @return * returneaza valoarea polinomului Bernstein B_{k,n}(t) in t, k - indice, n - ordin */ private static double fq1(double t) { return 2*t*(1-t); }
/** * Polinomul Bernstein de indice 2 si ordin 2 * @param t * @return * returneaza valoarea polinomului Bernstein B_{k,n}(t) in t, k - indice, n - ordin */ private static double fq2(double t) { return Math.pow(t, 2); }
public static void main(String[] args) { Point2D.Float P1 = new Point2D.Float(10,10); Point2D.Float PC = new Point2D.Float(30,50); Point2D.Float P3 = new Point2D.Float(15,20);
Point2D.Float bezPoints[] = getQuadInterpPoints(P1, PC, P3); System.out.println("Curba Bezier este definita de:"); System.out.println(bezPoints[0]); System.out.println(bezPoints[1]); System.out.println(bezPoints[2]); } }